ASSUNTO DA RECLASSIFICAÇÃO

Meus queridos e amados alunos do 8º ano (1, 2,3 e 4), segue abaixo o assunto e uma lista de exercícios para auxiliar nos seus estudos.

Abraços e boa sorte!

A soma de dois números é 12 e a diferença entre eles é 4. Quais são estes números?

Para a resolução de problemas como este que apresenta duas incógnitas desconhecidas, utilizamos um sistema de equações.
Chamamos de x o primeiro número (o maior) e de y o segundo número.
Pelo enunciado:
» soma de dois números é 12, ou seja: x+y = 12 ...I
» a diferença entre eles é 4, isto é : x-y = 4 .....II
A solução de um sistema de equações com duas variáveis é um par ordenado (x,y) de números reais que satisfaz as duas equações ( I e II ).
Verificando o par ordenado (8,4), notamos que satisfaz as duas equações:
8+4=12 e 8-4=4 , logo a solução do sistema é (8,4)

DEFINIÇÃO

Um sistema de equação do primeiro grau com duas incógnitas x e y, pode ser definido como um conjunto formado por duas equações do primeiro grau. Lembrando que equação do primeiro grau é aquela que em todas as incógnitas estão elevadas à potência 1. Eles são utilizados para determinar os valores de x e y nas equações com duas variáveis. A resolução dos sistemas consiste em estabelecer uma relação entre as equações e aplicar técnicas de resolução. Os sistemas de equações podem ser possível e determinado, acontece quando se tem uma única solução, ou seja, quando as retas formadas pelas equações se cruzam em um único ponto. E podem ser impossível quando as retas formadas pelas equações no gráfico são paralelas.

Os métodos usados na resolução de um sistema são: Adição e substituição.

• O método da adição deve ser utilizado nos sistemas em que existe a oportunidade de zerar uma das incógnitas. como está explicado no exemplo acima.
  
• O método da substituição consiste em trabalhar qualquer equação do sistema de forma a isolar uma das incógnitas, substituindo o valor isolado na outra equação.

PROBLEMAS:

Cláudio usou apenas notas de R$ 20,00 e de R$ 5,00 para fazer um pagamento de R$ 140,00. Quantas notas de cada tipo ele usou, sabendo que no total foram 10 notas?

R: X notas de R$20,00 e Y notas de R$5,00
Montando o sistema fica assim:

Para resolvermos este sistema, basta multiplicar uma das equações para que fique igual , mas com os sinais opostos.

1° passo: pegar a primeira equação e multiplicar por (-5) para tornar o Y igual e com sinal oposto para podermos simplificar o Y e ficar somente com uma incógnita para achar seu valor.

x+y = 10 *(-5)
-5x-5y = -50 ← Ficando assim a equação .

2° Passo: Somar a primeira equação com a segunda.

Resposta: Cláudio usou seis notas de R$20,00 e quatro notas de R$5,00.

I) Resolva o seguinte Sistema escolhendo a equação e a variável mais conveniente para aplicar o processo de substituição:

II) Resolva o seguinte Sistema escolhendo a equação e a variável mais conveniente para aplicar o processo de adição:

1º passo: vamos multiplicar a primeira linha por -1 para podermos cortar –2x com 2x.

2º passo: Substituir y = – 2, em qualquer um das equações acima e encontrar o valor de x.

3º passo: dar a solução do sistema.

S = { (4, -2) } .

        PROBLEMAS ENVOLVENDO SIATEMAS DE  1º GRAU

1, Na geladeira de Ana há 15 litros de refrigerante, dispostos tanto em garrafa de um lito e meio, quanto de 60ml. Qual a quantidade de garrafas de cada capacidade  sabendo-se que 13 é o total de garrafas?

Talvez a maior dificuldade ao resolvermos sistemas de equação do 1° grau com 2 incógnitas, não seja a resolução do sistema em si, pois basta escolhermos um dos dois métodos de resolução de sistemas apresentados aqui e pronto, mas sim a dificuldade de equacionarmos o sistema.

Neste problema estamos tratando de garrafas em duas capacidades: 1,5 l e 600 ml que convertidos em litros são 0,6 l. Sabemos também que temos um total de 15 l de refrigerante, acondicionados em 13 garrafas.
Então vamos montar duas equações. Uma tratando a quantidade de garrafas e outra tratando a quantidade de refrigerante.
Vamos atribuir x à quantidade de garrafas com capacidade de 1,5 l e y às garrafas de 0,6 l.
Segundo o enunciado temos x garrafas de 1,5 l e mais y garrafas de 0,6 l que totalizam 15 l. Então temos a primeira equação:



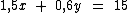
O enunciado também nos leva a concluir que temos x garrafas de 1,5 l e mais y garrafas de 0,6 l em um total de 13 garrafas. Temos então a segunda equação:


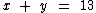
Eis portanto o nosso sistema:


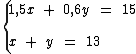
Para solucionarmos o problema pelo método da adição, vamos começar multiplicando todos os termos da segunda equação por -0,6:



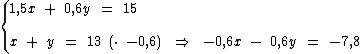
Escolhemos -0,6 por ser o oposto do coeficiente de y na primeira equação.
Repare agora que ao somarmos as duas equações estaremos eliminando a variável y:


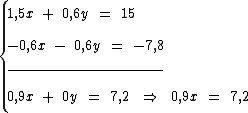
Agora para encontramos o valor de x, basta passarmos o coeficiente 0,9 para o segundo membro, dividindo o termo 7,2:


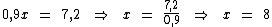
Agora que temos o valor de x, vamos substituir o x da segunda equação por 8 para encontrarmos o valor de y:



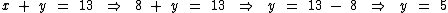
Portanto para ordenado (8, 5) é a solução do referido sistema.

Na geladeira de Ana há 8 garrafas de 1500 ml e 5 garrafas de 600 ml.

Resolver um sistema significa encontrar um par de valores das incógnitas X e Y que faça verdadeira as equações que fazem parte do sistema.

Exemplos:

a) O par (4,3 ) pode ser a solução do sistema

x – y = 2

x + y = 6

Para saber se estes valores satisfazem ao sistema, basta substituir os valores em ambas as equações:

x - y = 2 x + y = 6

4 – 3 = 1 4 + 3 = 7

1 ≠ 2 (falso) 7 ≠ 6 (falso)

A resposta então é falsa. O par (4,3) não é a solução do sistema de equações acima.

b) O par (5,3 ) pode ser a solução do sistema

x – y = 2

x + y = 8

Para saber se estes valores satisfazem ao sistema, basta substituir os valores em ambas as equações:

x - y = 2 x + y = 8

5 – 3 = 2 5 + 3 = 8

2 = 2 (verdadeiro 8 = 8 (verdadeiro)

A resposta então é verdadeira. O par (5,3) é a solução do sistema de equações acima.

* Métodos para solução de sistemas do 1º grau.

- Método de substituição

Esse método de resolução de um sistema de 1º grau estabelece que “extrair” o valor de uma incógnita é substituir esse valor na outra equação.

Observe:

x – y = 2

x + y = 4

Vamos escolher uma das equações para “extrair” o valor de uma das incógnitas, ou seja, estabelecer o valor de acordo com a outra incógnita, desta forma:

x – y = 2 ---> x = 2 + y

Agora iremos substituir o “X” encontrado acima, na “X” da segunda equação do sistema:

x + y = 4

(2 + y ) + y = 4

2 + 2y = 4 ----> 2y = 4 -2 -----> 2y = 2 ----> y = 1

Temos que: x = 2 + y, então

x = 2 + 1

x = 3

Assim, o par (3,1) torna-se a solução verdadeira do sistema.

- Método da adição

Este método de resolução de sistema do 1º grau consiste apenas em somas os termos das equações fornecidas.

Observe:

x – y = -2

3x + y = 5

Neste caso de resolução, somam-se as equações dadas:

x – y = -2

3x + y = 5 +

4x = 3

x = 3/4

Veja nos cálculos que quando somamos as duas equações o termo “Y” se anula. Isto tem que ocorrer para que possamos achar o valor de “X”.

Agora, e quando ocorrer de somarmos as equações e os valores de “x” ou “y” não se anularem para ficar somente uma incógnita ?

Neste caso, é possível usar uma técnica de cálculo de multiplicação pelo valor excludente negativo.

Ex.:

3x + 2y = 4

2x + 3y = 1

Ao somarmos os termos acima, temos:

5x + 5y = 5, então para anularmos o “x” e encontramos o valor de “y”, fazemos o seguinte:

» multiplica-se a 1ª equação por +2

» multiplica-se a 2ª equação por – 3

Vamos calcular então:

3x + 2y = 4 ( x +2)

2x + 3y = 1 ( x -3)

6x +4y = 8

-6x - 9y = -3 +

-5y = 5

y = -1

Substituindo:

2x + 3y = 1

2x + 3.(-1) = 1

2x = 1 + 3

x = 2

Verificando:

3x + 2y = 4 ---> 3.(2) + 2(-1) = 4 -----> 6 – 2 = 4

2x + 3y = 1 ---> 2.(2) + 3(-1) = 1 ------> 4 – 3 = 1