Os produtos notáveis aparecem com muita freqüência no cálculo algébrico. Esses produtos são conhecidos pelo nome de produtos notáveis. O termo “Produto” pode ser o resultado de uma função de multiplicação e o termo “notável” poder definido como “importante”, ou aquilo que se destaca.
Quadrado da soma de dois termos
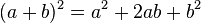 .
.
Regra básica: Quadrado do primeiro, mais duas vezes o primeiro vezes o segundo, mais o quadrado do segundo.[2]
- Exemplos:
[editar]Quadrado da diferença de dois termos
A expressão diferença do quadrado da soma apenas pelo sinal da segunda parcela:
Regra básica: Quadrado do primeiro termo, menos duas vezes o primeiro vezes o segundo , mais o quadrado do segundo

- Exemplos:
[editar]Produto da soma pela diferença de dois termos

Regra básica: Quadrado do primeiro termo menos o quadrado do segundo termo
- Exemplos:
[editar]Cubo da diferença de dois termos
Regra básica: É o cubo do 1° termo, menos 3 vezes o produto do quadrado do 1° termo pelo segundo, mais 3 vezes o produto do 1° termo pelo quadrado do 2° termo, menos o cubo do 2° termo.
- Exemplos:
[editar]Cubo da soma de dois termos
O cubo da soma de dois termos se diferencia do cubo da diferença apenas pelos sinais Regra básica: É o cubo do 1° termo, mais 3 vezes o produto do quadrado do 1°termo pelo segundo, mais 3 vezes o produto do 1° termo pelo quadrado do segundo termo, mais o cubo do segundo termo. 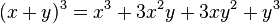
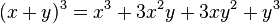
- Exemplos:
[editar]Quadrado da soma de três termos

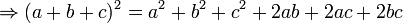
- Exemplos:


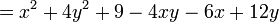
- Exercícios resolvidos de produtos notáveisa) (3x+y)2(3x+y)2 = (3x)2+2.3x.y+y2 = 9x2+6xy+y2b) ((1/2)+x2)2((1/2)+x2)2 = (1/2)2+2.(1/2).x2+(x2)2= (1/4) +x2+x4c) ((2x/3)+4y3)2((2x/3)+4y3)2 = (2x/3)2-2.(2x/3).4y3+(4y3)2= (4/9)x2-(16/3)xy3+16y6d) (2x+3y)3(2x+3y)3= (2x)3+3.(2x)2.3y+3.2x.(3y)2+(3y)3= 8x3+36x2y+54xy2+27y3
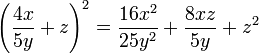

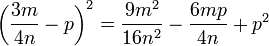

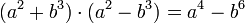




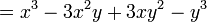


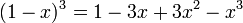


Nenhum comentário:
Postar um comentário