OPERAÇÕES COM POLINÔMIOS

Operações com polinômios 

Nas situações envolvendo cálculos algébricos, é de extrema importância a aplicação de regras nas operações entre os monômios. As situações a serem apresentadas abordarão a adição, a subtração e a multiplicação de polinômios.

Adição e Subtração

Considere os polinômios –2x² + 5x – 2 e –3x³ + 2x – 1. Vamos efetuar a adição e a subtração entre eles.

Adição

(–2x² + 5x – 2) + (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal

–2x² + 5x – 2 – 3x³ + 2x – 1 → reduzir os termos semelhantes

–2x² + 7x – 3x³ – 3 → ordenar de forma decrescente de acordo com a potência

–3x³ – 2x² + 7x – 3

Subtração

(–2x² + 5x – 2) – (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal

–2x² + 5x – 2 + 3x³ – 2x + 1 → reduzir os termos semelhantes

–2x² + 3x – 1 + 3x³ → ordenar de forma decrescente de acordo com a potência

3x³ – 2x² + 3x – 1



Multiplicação de polinômio por monômio

Para entendermos melhor, observe o exemplo:

(3x²) * (5x³ + 8x² – x) → aplicar a propriedade distributiva da multiplicação

15x⁵ + 24x⁴ – 3x³

 Multiplicação de polinômio por polinômio

Para efetuarmos a multiplicação de polinômio por polinômio também devemos utilizar a propriedade distributiva. Veja o exemplo:

(x – 1) * (x² + 2x - 6)


x² * (x – 1) + 2x * (x – 1) – 6 * (x – 1)

(x³ – x²) + (2x² – 2x) – (6x – 6)

x³ – x² + 2x² – 2x – 6x + 6 → reduzindo os termos semelhantes.

x³ + x² – 8x + 6

Portanto, nas multiplicações entre monômios e polinômios aplicamos a propriedade distributiva da multiplicação.

Polinômio é uma expressão algébrica composta por dois ou mais monômios. Na divisão de polinômios, utilizamos duas regras matemáticas fundamentais: realizar a divisão entre os coeficientes numéricos e divisão de potências de mesma base (conservar a base e subtrair os expoentes).
Quando trabalhamos com divisão, utilizamos também a multiplicação no processo. Observe o seguinte esquema:

 

 

Caso queira verificar se a divisão está correta, basta multiplicar o quociente pelo divisor, com vistas a obter o dividendo como resultado.

Verificando → quociente * divisor + resto = dividendo 4x * (3x² + x – 2) + 0
12x³ + 4x² – 8x

Caso isso ocorra, a divisão está correta. No exemplo a seguir, iremos dividir polinômio por polinômio. Veja:

Exemplo 2:

  

Verificando → quociente * divisor + resto = dividendo

(2x – 5) * (5x – 9) + (–5)
10x² – 18x – 25x + 45 + (–5)
10x² – 43x + 45 – 5
10x² – 43x + 40

 Observe o exemplo de número 3:

 

 Verificando → quociente * divisor + resto = dividendo
(3x² + x – 1) * (2x² – 4x + 5) + 0
6x4 – 12x³ + 15x² + 2x³ – 4x² + 5x – 2x² + 4x – 5
6x4 – 10x³ + 9x² + 9x – 5

 Exemplo 4:

 

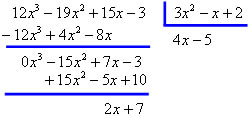
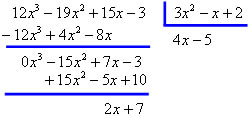
 Verificando → quociente * divisor + resto = dividendo
(4x – 5) * (3x² – x + 2) + (2x + 7)
12x³ – 4x² + 8x – 15x² + 5x – 10 + (2x + 7)
12x³ – 19x² + 13x – 10 + 2x + 7
12x³ – 19x² + 15x – 3