MATRIZES
- Definição: Uma matriz é um arranjo retangular de números variáveis, cada um tendo um lugar ordenado dentro da matriz. os números ou variáveis são chamados elementos da matriz.
- Através de parênteses ( );
- Através de colchetes [ ];
- Através de barras duplas II II.
Um elemento de uma matriz A que está na i-ésima linha e na j-ésima coluna é chamado de elemento i,j ou (i,j)-ésimo elemento de A. Ele é escrito como ai,j ou a[i,j]. Nesse exemplo, o elemento a1 2 é 2, o número na primeira linha e segunda coluna do quadro.
As entradas (símbolos) de uma matriz também podem ser definidas de acordo com seus índices i ej. Por exemplo, aij = i + j, para i de 1 a 3 e j de 1 a 2, define a matriz 3x2  .
.
 .
.CLASSIFICAÇÃO DE MATRIZES QUANTO AO NÚMERO DE COLUNAS OU LINHAS
Matriz quadrada
Uma matriz é dita quadrada se tem o mesmo número de linhas e colunas, ou seja, quando podemos dizer que, m tem a mesma quantidade de elementos que n. Numa matriz quadrada A de ordem n × n, chama-se de diagonal principal os elementos aij onde i = j, para i de 1 a n.Matriz identidade
A matriz identidade In é a matriz quadrada n × n que tem todos os membros da diagonal principal iguais a 1 e 0 nas outras posições. Exemplo: 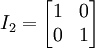 .
.
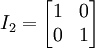 .
.A única matriz identidade que não contém zero é a matriz identidade de ordem 1: 
Matriz inversa
Uma matriz A − 1 é dita inversa de uma matriz A, se obedece à equação matricial A.A − 1 = I, ou seja, se o produto entre as matrizes é a matriz identidade. A analogia com os números reais é evidente, pois assim como o produto entre dois números inversos é a unidade (elemento neutro da multiplicação), o produto entre duas matrizes inversas é a matriz identidade (elemento neutro da multiplicação entre matrizes). Uma matriz que possui inversa é dita inversível.
Matriz transposta
A matriz transposta de uma matriz Am × n é a matriz Atn × m em que , ou seja, todos os elementos da primeira linha, tornar-se-ão elementos da primeira coluna, todos os elementos da segunda linha, tornar-se-ão elementos da segunda coluna, todos os elementos da n linha, tornar-se-ãoelementos da n coluna. Exemplo:
, ou seja, todos os elementos da primeira linha, tornar-se-ão elementos da primeira coluna, todos os elementos da segunda linha, tornar-se-ão elementos da segunda coluna, todos os elementos da n linha, tornar-se-ãoelementos da n coluna. Exemplo: 
Multiplicação por um escalar
A multiplicação por um escalar é uma das operações mais simples que podem ser feitas com matrizes. Para multiplicar um número k qualquer por uma matriz n×m A, basta multiplicar cada entrada aij de A por k. Assim, a matriz resultante B será também n×m e bij = k.aij. Com isso, pode-se pensar também na noção de dividir uma matriz por um número: basta multiplicá-la pelo inversodesse número. Mas essa noção pode ser perigosa: enquanto a multiplicação entre um número e uma matriz pode ser dita "comutativa", o mesmo não vale para a divisão, pois não se pode dividir um número por uma matriz.
Por exemplo:
[editar]Adição e subtração entre matrizes
Dado as matrizes A e B do tipo m por n, sua soma A + B é a matriz m por n computada adicionando os elementos correspondentes: (A + B)[i,j] = A[i, j] + B[i,j].
Por exemplo:
Para melhorar a forma de calcular, você pode reescrever a segunda matriz, revertendo seus elementos, onde o elemento (-1) passará para (1) e o elemento (2) passará para (-2) e assim sucessivamente. Após feito isso, além de fazer A-B, você usará A+B.
Multiplicação de matrizes
Multiplicação de duas matrizes é bem definida apenas se o número de colunas da matriz da esquerda é o mesmo número de linhas da matriz da direita. Se A é uma matriz m por n e B é uma matriz n por p, então seu produto AB é a matriz m por p (m linhas e p colunas) dada por:
para cada par i e j.
Por exemplo:
É importante notar que a comutatividade não é garantida; isto é, dadas as matrizes A e B com seu produto definido, então geralmente AB ≠ BA.
As matrizes são estruturas matemáticas organizadas na forma de tabela com linhas e colunas, utilizadas na organização de dados e informações. Nos assuntos ligados à álgebra, as matrizes são responsáveis pela solução de sistemas lineares. Elas podem ser construídas com m linhas e n colunas, observe:
.jpg) , matriz de ordem 3 x 2. (3 linhas e 2 colunas)
, matriz de ordem 3 x 2. (3 linhas e 2 colunas).jpg) , matriz de ordem 4 x 2. (4 linhas e 2 colunas)
, matriz de ordem 4 x 2. (4 linhas e 2 colunas)As matrizes com número de linhas e colunas iguais são denominadas matrizes quadradas. Observe:
.jpg) , matriz quadrada de ordem 3 x 3.
, matriz quadrada de ordem 3 x 3..jpg) , matriz quadrada de ordem 4 x 4.
, matriz quadrada de ordem 4 x 4.Na matriz .jpg) , temos que cada elemento ocupa seu espaço de acordo com a seguinte localização:
, temos que cada elemento ocupa seu espaço de acordo com a seguinte localização:
O elemento 2 está na 1ª linha e 1ª coluna.
O elemento 5 está na 1ª linha e 2ª coluna.
O elemento 7 está na 2ª linha e 1ª coluna.
O elemento –9 está na 2ª linha e 2ª coluna.
O elemento 5 está na 1ª linha e 2ª coluna.
O elemento 7 está na 2ª linha e 1ª coluna.
O elemento –9 está na 2ª linha e 2ª coluna.
Portanto, temos:
aij, onde i = linhas e j = colunas.
a11 = 2
a12 = 5
a21 = 7
a 22 = –9
a11 = 2
a12 = 5
a21 = 7
a 22 = –9
Podemos construir uma matriz de acordo com uma lei de formação baseada em situações variadas. Por exemplo, vamos construir uma matriz de ordem 3 x 3, seguindo a orientação aij = 3i + 2j.
.jpg)
Vamos escrever a matriz B dada por (aij)4x4, de modo que i + j, se i = j e i – j, se i ≠ j.
.jpg)
Aplicação da definição de inversa
Este método de procura da inversa consiste em partir de uma matriz quadrada genérica, com incógnitas em vez de valores e aplicar a seguinte propriedade:
- Exemplo
Se queremos descobrir a inversa da matriz  de dimensões 2 x 2 representada abaixo recorremos a uma matriz genérica que nos permitirá multiplicar as matrizes:
de dimensões 2 x 2 representada abaixo recorremos a uma matriz genérica que nos permitirá multiplicar as matrizes:
 de dimensões 2 x 2 representada abaixo recorremos a uma matriz genérica que nos permitirá multiplicar as matrizes:
de dimensões 2 x 2 representada abaixo recorremos a uma matriz genérica que nos permitirá multiplicar as matrizes:Associamos símbolos arbitrariamente à inversa da nossa matriz original – nosso objectivo é determinar os valores de a, b, c e d. Para isso aplicaremos a definição de inversa:
Resolvendo essa multiplicação de matrizes somos conduzidos a um sistema de equações:
Logo:
Adição
As matrizes envolvidas na adição devem ser da mesma ordem. E o resultado dessa soma será também outra matriz com a mesma ordem.
Assim podemos concluir que:
Se somarmos a matriz A com a matriz B de mesma ordem, A + B = C, teremos como resultado outra matriz C de mesma ordem e para formar os elementos de C somaremos os elementos correspondentes de A e B, assim: a11 + b11 = c11.
Exemplos:
Dada a matriz A= 3 x 3 e matriz B=
3 x 3 e matriz B=  3 x 3, se somarmos a A + B, teremos:
3 x 3, se somarmos a A + B, teremos:
 +
+.jpg) =
= .jpg) 3 x 3
3 x 3
Observe os elementos em destaques:
a13 = - 1 e b13 = - 5 ao somarmos esses elementos chegaremos a um terceiro que é o
c13 = -6. Pois -1 + (-5) = -1 – 5 = - 6
O mesmo ocorre com os outros elementos, para chegarmos ao elemento c32, tivemos que somar a32 + b32. Pois, 3 + (-5) = 3 – 5 = - 2
Assim: A + B = C, onde C tem a mesma ordem de A e B.
►Subtração
As duas matrizes envolvidas na subtração devem ser da mesma ordem. E a diferença delas deverá dar como resposta outra matriz, mas de mesma ordem.
Assim temos:
Se subtrairmos a matriz A da matriz B de mesma ordem, A – B = C, obteremos outra matriz C de mesma ordem. E para formarmos os elementos de C, subtrairemos os elementos de A com os elementos correspondentes de B, assim: a21 – b21 = c21.
Exemplos:
Dada a matriz A = 3 x 3 e B =
3 x 3 e B = 3 x 3, se subtrairmos A – B, teremos:
3 x 3, se subtrairmos A – B, teremos:
 -
- 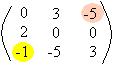 =
=  3 x 3
3 x 3
Observe os elementos destacados:
Quando subtraímos a13 – b13 = c13, -1 – (-5) = -1 + 5 = 4
Quando subtraímos a31 – b31 = c31, - 4 – (-1) = -4 + 1 = -3
Assim A – B = C, onde C é uma matriz de mesma ordem de A e B.
As matrizes envolvidas na adição devem ser da mesma ordem. E o resultado dessa soma será também outra matriz com a mesma ordem.
Assim podemos concluir que:
Se somarmos a matriz A com a matriz B de mesma ordem, A + B = C, teremos como resultado outra matriz C de mesma ordem e para formar os elementos de C somaremos os elementos correspondentes de A e B, assim: a11 + b11 = c11.
Exemplos:
Dada a matriz A=
.jpg) =
= .jpg) 3 x 3
3 x 3 Observe os elementos em destaques:
a13 = - 1 e b13 = - 5 ao somarmos esses elementos chegaremos a um terceiro que é o
c13 = -6. Pois -1 + (-5) = -1 – 5 = - 6
O mesmo ocorre com os outros elementos, para chegarmos ao elemento c32, tivemos que somar a32 + b32. Pois, 3 + (-5) = 3 – 5 = - 2
Assim: A + B = C, onde C tem a mesma ordem de A e B.
►Subtração
As duas matrizes envolvidas na subtração devem ser da mesma ordem. E a diferença delas deverá dar como resposta outra matriz, mas de mesma ordem.
Assim temos:
Se subtrairmos a matriz A da matriz B de mesma ordem, A – B = C, obteremos outra matriz C de mesma ordem. E para formarmos os elementos de C, subtrairemos os elementos de A com os elementos correspondentes de B, assim: a21 – b21 = c21.
Exemplos:
Dada a matriz A =
Observe os elementos destacados:
Quando subtraímos a13 – b13 = c13, -1 – (-5) = -1 + 5 = 4
Quando subtraímos a31 – b31 = c31, - 4 – (-1) = -4 + 1 = -3
Assim A – B = C, onde C é uma matriz de mesma ordem de A e B.
Um abraço!




![(AB)[i,j] = A[i,1] B[1,j] + A[i,2] B[2,j] + ... + A[i,n] B[n,j] \,\!](http://upload.wikimedia.org/wikipedia/pt/math/7/a/4/7a424a2f2bfee1127fbfc48750aa5132.png)
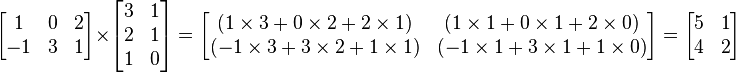






Nenhum comentário:
Postar um comentário